CIENCIAS BÁSICAS

COMPETENCIA ESPECÍFICA DE LA ASIGNATURA

Aplica los conceptos de la teoría de la probabilidad y estadística para organizar, clasificar, analizar e interpretar datos para la toma decisiones en aplicaciones de ingeniería biomédica, en computación y comunicaciones.

CARACTERIZACIÓN DE LA ASIGNATURA

Esta asignatura aporta al perfil del Ingeniero en las áreas referentes a la computación, comunicaciones y de Ingeniería Biomédica las competencias que le permitan entender, aplicar y desarrollar modelos matemáticos utilizando técnicas de probabilidad y estadística para el análisis de información y la toma de decisiones en las diferentes áreas de las ciencias computacionales.

La asignatura se encuentra ubicada al principio de la carrera. Probabilidad y Estadística consiste en los conceptos básicos de la teoría de la probabilidad y la estadística descriptiva de datos agrupados y no agrupados. Se enseña como razonar de manera lógica la toma decisiones en presencia de incertidumbre y variación.

El programa de este curso incluye el estudio y aplicación de las técnicas de la Estadística, aporta los conceptos y métodos de Probabilidad, modela fenómenos aleatorios, resuelve problemas reales, hace inferencias, respalda la toma de decisiones, estudia variables aleatorias, tanto de tipo discreto como de tipo continuo por lo que apoya a las asignaturas de Formulación y Evaluación de Proyectos. Probabilidad y Estadística provee los conocimientos básicos sobre conceptos de probabilidad y pruebas estadísticas para la asignatura de Simulación, para la asignatura de Investigación de operaciones los temas de estadística descriptiva y distribuciones de probabilidad, para la asignatura de Matemáticas para la Toma de Decisiones los temas de probabilidad y estadística le dan la introducción a teoría de inventarios. Por lo que se pueden desarrollar proyectos integradores con cualquiera de esas asignaturas.

COMPETENCIA ESPECÍFICA DE LA ASIGNATURA

Investiga y aplica los conocimientos de física elemental, así como las herramientas fundamentales para la realización de proyectos que coadyuven en el desarrollo de las comunidades.

CARACTERIZACIÓN DE LA ASIGNATURA

Esta asignatura aporta al perfil del Ingeniero en Desarrollo Comunitario la capacidad para explicar fenómenos físicos involucrados en los diversos proyectos para el desarrollo de la comunidad. La presente asignatura incluye conceptos relacionados con estática y dinámica de partículas, Leyes de Newton y mecánica de fluidos, así como sus aplicaciones las cuales deberán enfocarse en la solución de problemas presentes en el desarrollo de proyectos relacionados con la comunidad.

 Para integrarla, se ha hecho un análisis identificando los temas básicos que debe dominar un Ingeniero en Desarrollo Comunitario en su quehacer profesional y que le permitirán tomar decisiones y acciones asertivas en las diferentes actividades en que participe. 

 La presente asignatura es insertada en el primer tercio de la trayectoria escolar y será la base para el estudio de temas tales como: diseño de sistemas de riego para diversos cultivos, diseño de instalaciones de diversos tipos, diseño y ejecución de experimentos, y el principal, uso sustentable de los recursos disponibles en la naturaleza.

CARACTERIZACIÓN DE LA ASIGNATURA

Esta asignatura contiene los temas básicos e importantes para introducir al estudiante en el estudio del cálculo, necesario en toda ingeniería; se estudian los conceptos de: números reales, variables, funciones y límites, con los que se podrá establecer uno de los más esenciales, la derivada, concepto que permite analizar la razón de cambio entre variables. 

Esta noción es de trascendental importancia en las aplicaciones de la ingeniería. El Cálculo Diferencial contribuye a que el estudiante adquiera conocimientos necesarios para asimilar las asignaturas de Cálculo Integral, Cálculo Vectorial, Ecuaciones Diferenciales, Métodos Numéricos, asignaturas de Física y Ciencias de la Ingeniería. Además, contiene los principios y bases para el modelado matemático.

 La asignatura de Cálculo Diferencial se organiza en cuatro temas: 

 El primer tema inicia con una descripción de los números reales y sus distintos subconjuntos. Se define el concepto de función real de una variable real y se describen los diferentes tipos de funciones algebraicas y trascendentes, incluye el estudio del dominio y rango de funciones, su representación gráfica, así como las operaciones y transformaciones rígidas y no rígidas. También se estudia la simetría de las funciones (funciones pares e impares), las definidas por más de una regla de correspondencia, las funciones inversas, hasta llegar a la formulación de funciones como modelos matemáticos en distintos contextos. 

 En el tema dos se introduce la noción intuitiva de límite mediante el enfoque informal. Se aborda el cálculo de límites por evaluación directa y de aquellos que requieren de estrategias algebraicas como factorización o racionalización, se continúa con límites trigonométricos y los límites unilaterales. Se incluyen casos especiales de límites infinitos y límites al infinito, así como la identificación de asíntotas horizontales y verticales en la gráfica de una función. El tema concluye con el concepto y estudio de la continuidad de una función en un punto y en un intervalo.

En el tema tres, se aborda de manera geométrica el problema de la recta tangente a una curva en un punto, para posteriormente, mediante la regla de los cuatro pasos hallar derivadas de distintas funciones algebraicas. Luego, se define la derivada como un límite y se utiliza dicho concepto para deducir las reglas de derivación y con ellas la derivada de una función. Se utiliza la regla de la cadena para derivar funciones compuestas. 

El tema cuatro trata sobre las aplicaciones de la derivada, el análisis de una función a partir de la determinación de sus puntos críticos, intervalos donde una función es creciente o decreciente, valores extremos, puntos de inflexión e intervalos donde exista concavidad hacia arriba o hacia abajo, que permitan construir su gráfica. Se abordan problemas a través del modelado de situaciones que requieren de la determinación de una función real y de la derivada para obtener soluciones óptimas. Se continúa con la construcción del concepto de diferencial y su interpretación para calcular aproximaciones específicas. Se concluye con la aplicación de la regla de L´Hôpital en el cálculo de límites indeterminados.

En este curso se estará viendo los siguientes Temas:

Profesora : Jannet Adonay Dillman Hernández

En este curso se estará viendo los siguientes Temas:

1. Conceptos fundamentales en Química Orgánica
   
2. Hidrocarburos
   
3. Grupos funcionales
   
4. Estereoquímica
   
5. Química Orgánica en la Industria.
   

 En este curso se estará viendo los siguientes Temas:

1. La materia y sus cambios
   
2. Clasificación periódica de los elementos
   
3. Nociones sobre enlace químico
   
4. Reacciones químicas y estequiometría
   
5. Equilibrio químico.
   
6. Compuestos Orgánicos
   

ÁLGEBRA LINEAL 

El Álgebra Lineal aporta al perfil del ingeniero la capacidad para desarrollar un pensamiento lógico, heurístico y algorítmico al modelar fenómenos de naturaleza lineal y resolver problemas.

Esta asignatura proporciona al estudiante de ingeniería una herramienta para resolver problemas de aplicaciones de la vida ordinaria y de aplicaciones de la ingeniería. 

Muchos fenómenos de la naturaleza, que se presentan en la ingeniería, se pueden aproximar a través de un modelo lineal. Esta asignatura nos sirve para caracterizar estos fenómenos y convertirlos en un modelo lineal ya que es más accesible, de allí la importancia de estudiar Álgebra Lineal.

Esta asignatura proporciona además conceptos matemáticos relacionados con Cálculo Vectorial, Ecuaciones Diferenciales, Investigación de Operaciones y en otras asignaturas de especialidad por lo que se pueden diseñar proyectos integradores con cualquiera de ellas.

Cálculo Vectorial 

La asignatura contribuye a desarrollar un pensamiento lógico-matemático al perfil del ingeniero y aporta las herramientas básicas para introducirse al estudio del cálculo vectorial y su aplicación, así como las bases para el modelado matemático. Además, proporciona herramientas que permiten modelar fenómenos de contexto.

 La importancia del estudio del Cálculo Vectorial radica principalmente en que en diversas aplicaciones de la ingeniería, la concurrencia de variables espaciales y temporales, hace necesario el análisis de fenómenos naturales cuyos modelos utilizan funciones vectoriales o escalares de varias variables.

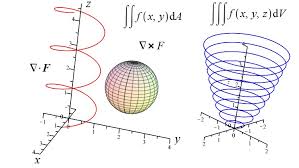
 La asignatura está diseñada de manera que el estudiante pueda representar conceptos, que aparecen en el campo de la ingeniería por medio de vectores; resolver problemas en los que intervienen variaciones continuas; resolver problemas geométricos en forma vectorial; graficar funciones de varias variables; calcular derivadas parciales; representar campos vectoriales que provengan del gradiente de un campo escalar, así como su divergencia y rotacional; resolver integrales dobles y triples; aplicar las integrales en el cálculo de áreas y volúmenes.

 Con esta asignatura se espera desarrollar la capacidad de análisis y síntesis en actividades de modelación matemática; adquirir estrategias para resolver problemas; elaborar desarrollos analíticos para la adquisición de un concepto; pensar conceptualmente, desarrollar actitudes para la integración a grupos interdisciplinarios; aplicar los conocimientos adquiridos a la práctica y aprovechar los recursos que la tecnología ofrece, como el uso TIC’s.

Esta asignatura sirve como base para otras asignaturas de las diferentes especialidades tales como: estática, dinámica y mecanismos, con la representación geométrica y álgebra de vectores; electromagnetismo y teoría electromagnética con el cálculo del gradiente, divergencia y rotacional de un campo vectorial; en termodinámica con el cálculo de derivadas parciales en las diferentes formas de la segunda ley; en fenómenos de transporte, transferencia de masa y transferencia de calor, con el cálculo de derivadas parciales y las ecuaciones que modelan estos fenómenos. Se pueden diseñar proyectos integradores con cualquiera de ellas.

Profesora:  Jannet Adonay Dillman Hernández

En este curso se estará viendo los siguientes Temas:

Ecuaciones Diferenciales

Esta asignatura consolida su formación matemática como ingeniero y potencia su capacidad en el campo de las aplicaciones, aportando al perfil del ingeniero una visión clara sobre el dinamismo de la naturaleza. Además, contribuye al desarrollo de un pensamiento lógico, heurístico y algorítmico al modelar sistemas dinámicos.

El curso de ecuaciones diferenciales es un campo fértil de aplicaciones ya que una ecuación diferencial describe la dinámica de un proceso; el resolverla permite predecir su comportamiento y da la posibilidad de analizar el fenómeno en condiciones distintas. Esta es la asignatura integradora en los temas de matemáticas y pueden diseñarse proyectos integradores con asignaturas que involucren sistemas dinámicos para cada una de las ingenierías.

La característica más sobresaliente de esta asignatura es que en ella se aplican todos los conocimientos previos de las matemáticas.

   Profesor:  Jannet Adonay Dillman Hernández

 En este curso se estará viendo los siguientes Temas:

1. Elementos químicos
2. Enlaces químicos y propiedades de los compuestos.
   
3. Compuestos químicos inorgánicos
   
4. Estequiometría
   
5. Compuestos químicos orgánicos, estructura nomenclatura y propiedades